Sunday Times Teaser 3058 – Total Resistance
by Peter Good
Published Sunday May 02 2021 (link)
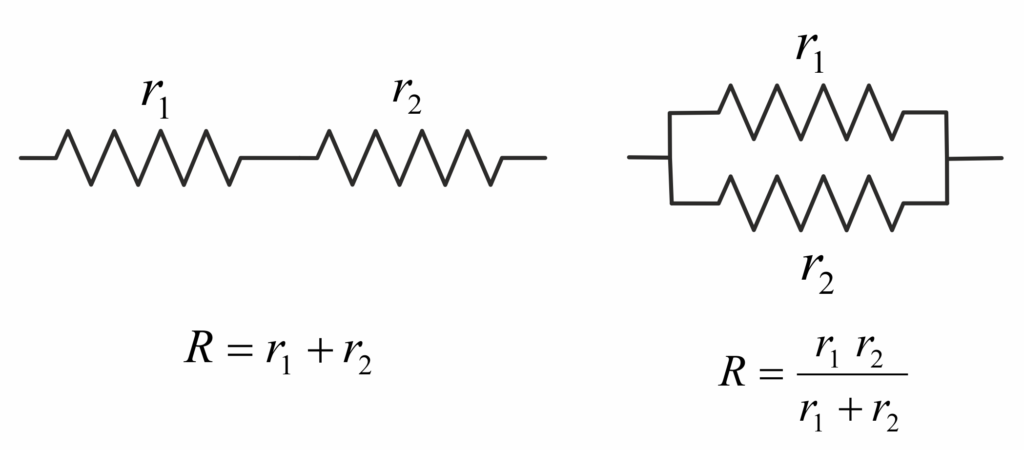
A physics teacher taught the class that resistors connected in serial have a total resistance that is the sum of their resistances while resistors connected in parallel have a total resistance that is the reciprocal of the sum of their reciprocal resistances, as shown in the diagrams. Each pupil was told to take five 35-ohm resistors and combine all five into a network. Each pupil then had to calculate theoretically and check experimentally the resistance of his or her network. Every network had a different resistance and the number of different resistances was the maximum possible. The total sum of these resistances was a whole number.
How many pupils were there in the class and what was the sum of the resistances?
Several assumptions have to be made in solving this teaser. Firstly, should we assume that all resistors have to be connected into the network at both their ends? Secondly, should we require that all resistors contribute to the overall resistance? The latter is important since there is a configuration in which one resistor is a part of the network but its presence doesn’t change the overall resistance. There is an option in the program to include or exclude this network configuration.
setting add_bridge = True produces an error
I would consider the bridged configuration valid, similar to a ‘Wheatstone bridge’.
Thanks for catching this, updated now.
No recursion but neither a general solving method.